planar-incr-embed concepts deep dive

For the past (almost) 6 months, I (Ellen Emilia Anna Zscheile (fogti)) worked on developing the planar-incr-embed crate, and worked on building a new routing backend for Topola based upon that, which uses a much smaller navigation mesh than the original routing backend.

Terminology

In this article, “etched path” will refer to routes / rubber band paths across a PCB which can’t be intersected by other paths. “holes” refer to unroutable sections of the PCB (which are the start and end of a path, but can’t be crossed otherwise), in particular, all “primal” vertices, i.e. FixedDots, polygons and Vias.

Motivation

The inspiration for this subproject were considerations about the fundamental group of planes (2D euclidean space) with holes in it (which can’t be crossed by etched paths). This lead to the realization that a voronoi diagram (in particular, the edges in that diagram) represent almost all routable paths (except those around the outer vertices).

Another important realization was that when looking at a segment of the plane without holes (but possibly surrounded by holes), and selecting an arbitrary point (outside of all holes), then taking an arbitrary closed simple (it has an injective parametrization) curve around the point such that the curve doesn’t enclose any holes (which might be sources/sinks), and recording all the etched paths that intersect with the curve in the order they get encountered by the injective parametrization, then an iteration over that sorted list of encounters has the following invariant if none of the etched paths intersect (meaning they are a planar embedding of etched paths):

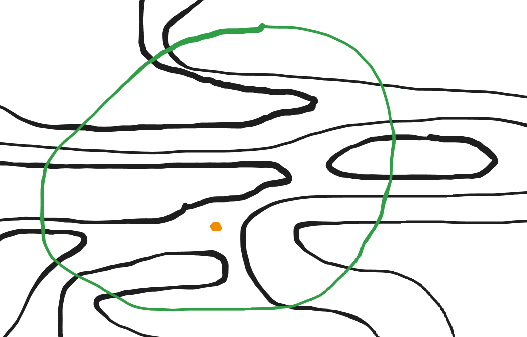
Let s be a stack of etched path labels. Let i be the next etched path in the list. If i is on the top of the stack s, pop it from the stack, otherwise, push it to the stack (see also handle_lifo, which implements this step). Then, repeat with the next etched path in the list (abort if the list is empty; later, we will also yield if s was empty after a pop).

Then, after iterating over the whole list like that, the stack will be empty. This is a LIFO.

Navmesh generation

In planar_incr_embed::navmesh::NavmeshSer::from_triangulation, we generate the planar-incr-embed Navmesh. It is a combination of several graphs:

• Voronoi diagram (Voronoi nodes and edges): The Voronoi diagram induces DualInner nodes and edges between those nodes, and also DualOuter nodes and edges between DualInner-DualOuter nodes.
• The primal nodes, including connections to those Delaunay faces that are their neighbors, respectively
• Edges between the different DualOuter nodes, induced by the convex hull of the Delaunay triangulation

The actual navmesh then gets generated by converting NavmeshSer into Navmesh via the From::from implementation, which converts the navmesh from the easily readable form into one which is more compact in memory, especially when using our A*-like search algorithm PmgAstar.

In the Navmesh / NavmeshRef / NavmeshRefMut implementation, there are both combined methods to look up edge data (edge_data_mut), and ones which split that into the lookup of the edge index + direction (resolve_edge_data) and the transformation of the edge index into the directed edge paths (access_edge_data_mut). Of course, non-_mut variants of edge_data_mut and access_edge_data_mut also exist.

Incremental construction of etched paths

In order to construct new etched paths on this planar “topological” navmesh, we need a way to compute where a given path could lead to next, given an entry location into a segment (Dual vertex). This is done by planar_incr_embed::navmesh::Navmesh::planarr_find_all_other_ends / its backend implementation planar_incr_embed::planarr::find_all_other_ends. It does what is described in the Motivation section above (it also yields if s was empty after a pop).

In order to be able to encode stuff into the navmesh that does influence the location of etched paths, but doesn’t modify its homotopy class and isn’t a path itself (so doesn’t follow the rule that it can’t be crossed), the enum planar_incr_embed::RelaxedPath, and in particular its Weak variant exists, which denotes exactly that (etched paths are then the Normal variant).

An usage example can be seen in the PmgAstar implementation.

Tangents to polygons

To be able to implement comparatively fast routing, we need an algorithm to find the tangents to a polygon given a single origin point (through which the tangents should pass). This is implemented in PR #201.

The idea here is to take the counter-clockwise angle between two polygon segments (of the convex hull of the polygon) with one point in common, and check if the beam towards the origin point lies inside that arc or not. The segments of true and false results of this check are contiguous when treating the list of them as being periodic (just like the polygon convex hull is). Then we can find the bounds of these two segments by:

1. doing a binary breadth-first search in order to find at least one true and one false entry, and then
2. doing an binary search to find the largest index which has the same value (for each of [false, true]).

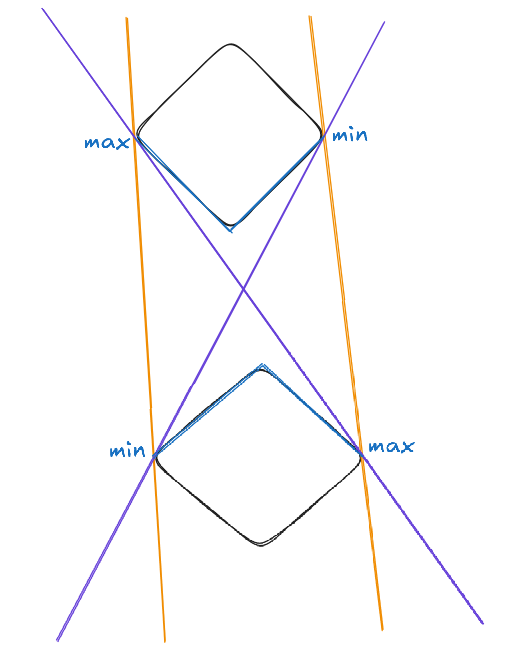
The part of each rectangle which faces towards the other is marked in blue, and it includes the points on the sides of the rectangles. The blue and non-blue (black) parts of the rectangles are the contiguous segments where the check mentioned above either returns true or false.