June 2025 Development Update
Category:
After the last development update, NLnet granted us additional 10 000 EUR for new tasks. For this money, we have implemented some experimental features, which are covered in the below sections.
Meanwhile, we are also working hard to complete all the unfinished features and fix as many bugs as possible to release Topola v0.1, the first alpha version of the Topola PCB router, which we hope to accomplish by the end of this year.
Exact lineocircular 2D geometry kernel
Implemented by Mikołaj Wielgus (mikolaj) in repository topola/cyrk.
Many electronic design applications (EDAs) for PCB design, including Topola, allow having geometrical objects whose shapes contain (thick) circular arcs. Unfortunately, many of the popular geometry libraries, notably iOverlay and Angus Johnson’s Clipper and Clipper2 libraries, operate only on geometries consisting of straight line segments and thus do not support circular arcs.
To work around this limitation, EDAs tend to instead implement circular arcs by approximating them with dense connected sequences of line segments (polylines) and representing them with floating point numbers. These solutions are not exact and hence predictably suffer from lack of numerical robustness, which leads to difficult bugs in edge cases.
In Topola, this problem is particularly likely to cause trouble because unlike other open-source EDAs, Topola exclusively routes rubberband traces, which are taut and thus fit tightly to constraints, leaving hardly any room for even small errors. This may impede finding optimal paths, and may even result in Topola failing to find any route at all.
To overcome this problem, we have created Cyrk, an exact lineocircular 2D geometry kernel. This new library allows calculation of intersections between lines, line segments, circles, and circle arcs, as well as union (OR) and intersection (AND) boolean operations on convex polygons whose sides can both be line segments and circle arcs (we call such geometrical objects convex lineocircular polygons), and also detection if a given point is contained inside any such convex lineocircular polygon. All this is done without involvement of any approximations. Such exact computation is achieved by having each coordinate of a point stored in multiple integers representing the roots of a quadratic equation with integer coefficients (such roots are also known as quadratic numbers) instead of just a single integer or floating point number.
You can see Cyrk in action on the following screenshot, which shows construction of intersections (yellow-colored contours) of two pairs of convex lineocircular polygons (brown-colored contours). The locations of the vertices and sides of the intersections had been calculated exactly, and were only approximated into floating points for the purpose of rendering only after all of the Cyrk’s calculations were completed. The inside of each contour is also filled with a stitch of gray points to show detection of whether a point is contained inside:
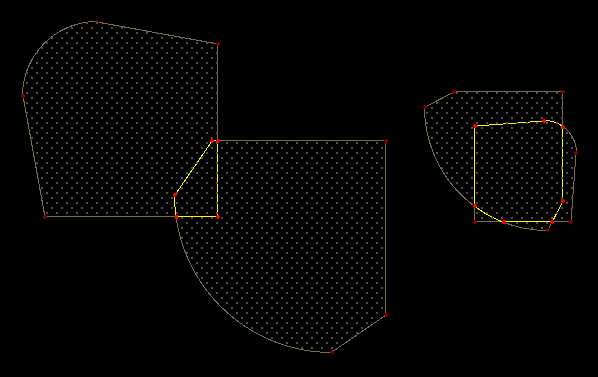
Cyrk, while functional, is not yet packaged or integrated in Topola.
Routing on an alternative navigation mesh
Implemented by Ellen Emilia Anna Zscheile (fogti) in PR #161.
To find the shortest path to route the trace on, Topola uses a pathfinding algorithm called Theta*, which is an enchanced version of the classic A* search algorithm. To supply this algorithm with a graph to operate on, every time before routing starts, Topola creates a navigation mesh (navmesh) by performing a Delaunay triangulation with some further custom processing. This method results in navmesh that looks like this (gray lines):
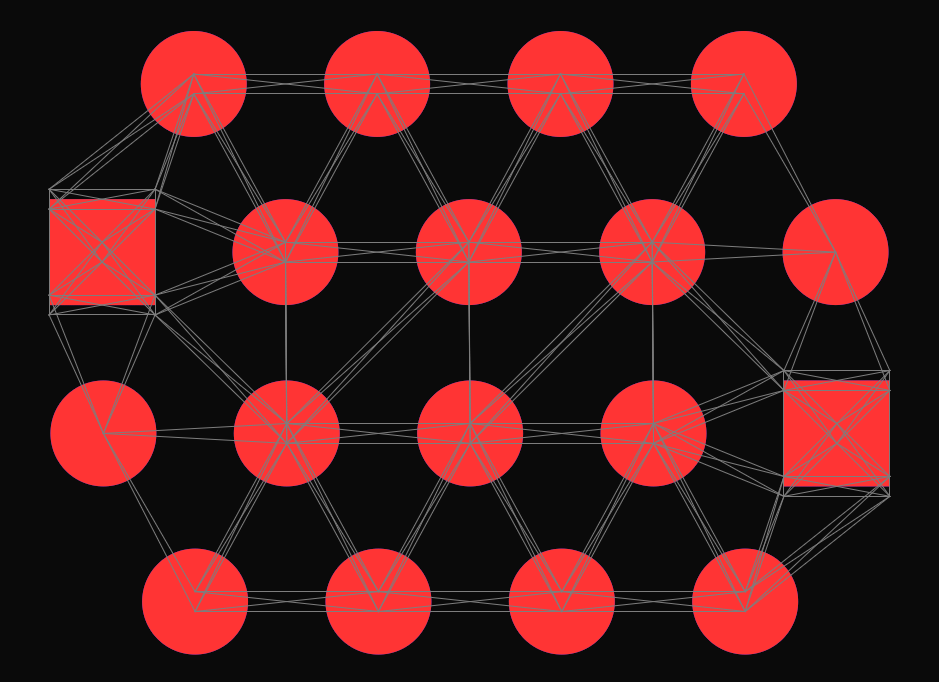
(You may see two visualizations how Topola uses the navmesh afterwards to guide the currently routed trace in a past blog post. Both visualizations are somewhat outdated; some improvements were made to the search algorithm since then.)
The above is not the only kind of navmesh that can be used. Since the last blog post, we have been developing an alternative routing method that operates on a navmesh created from a Voronoi diagram instead of a Delaunay triangulation. This new, alternative navmesh looks like this (yellow lines):
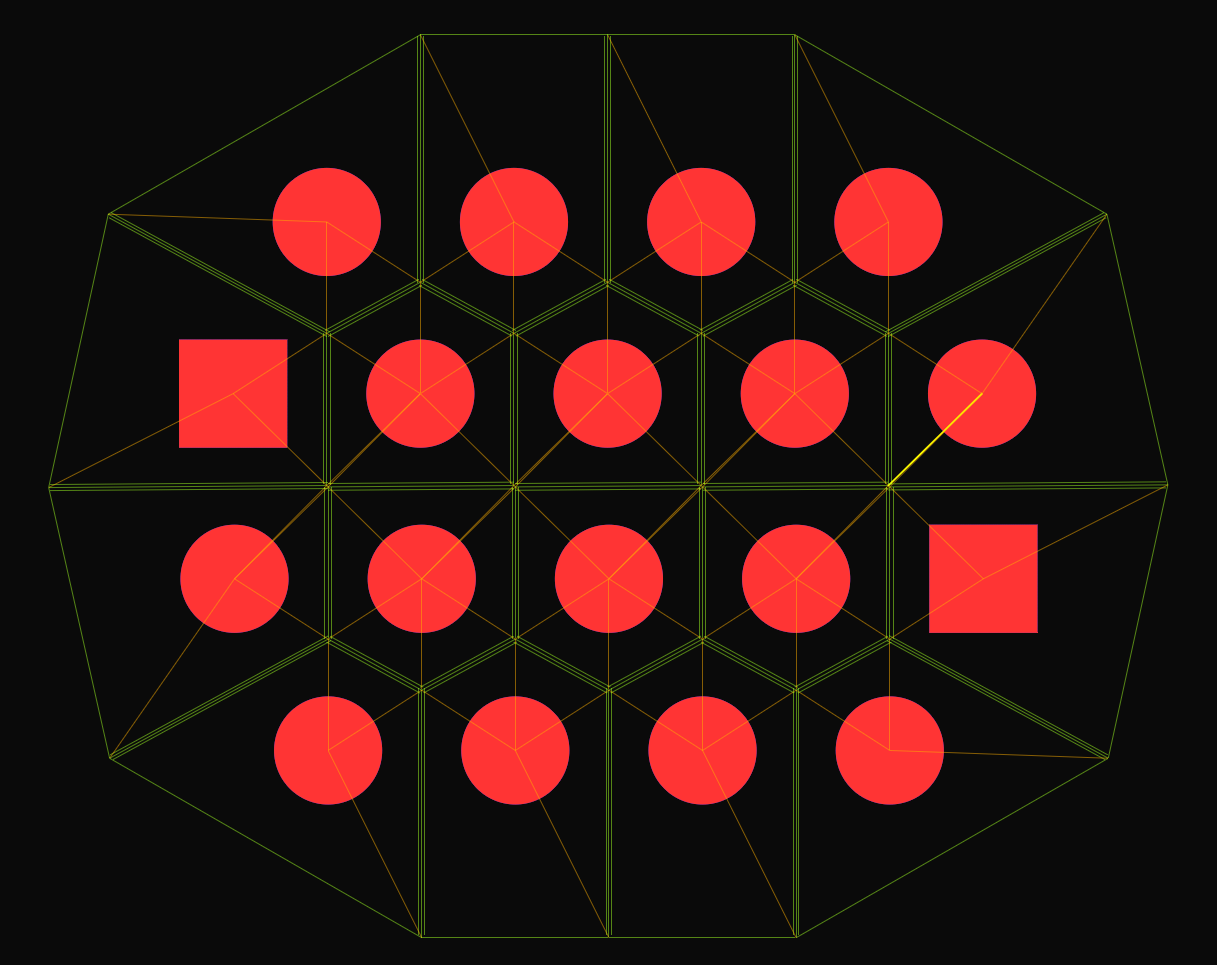
You can watch routing on this alternative navmesh in action on the following screencast:

You may also find some technical explanations of this alternative routing method in our documentation.